Principal component analysis¶
wiki: https://en.wikipedia.org/wiki/Principal_component_analysis
Principal component analysis (PCA) is a statistical procedure that uses an orthogonal linear transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components.
This transformation is defined in such a way that the first principal component has the largest possible variance, and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components.
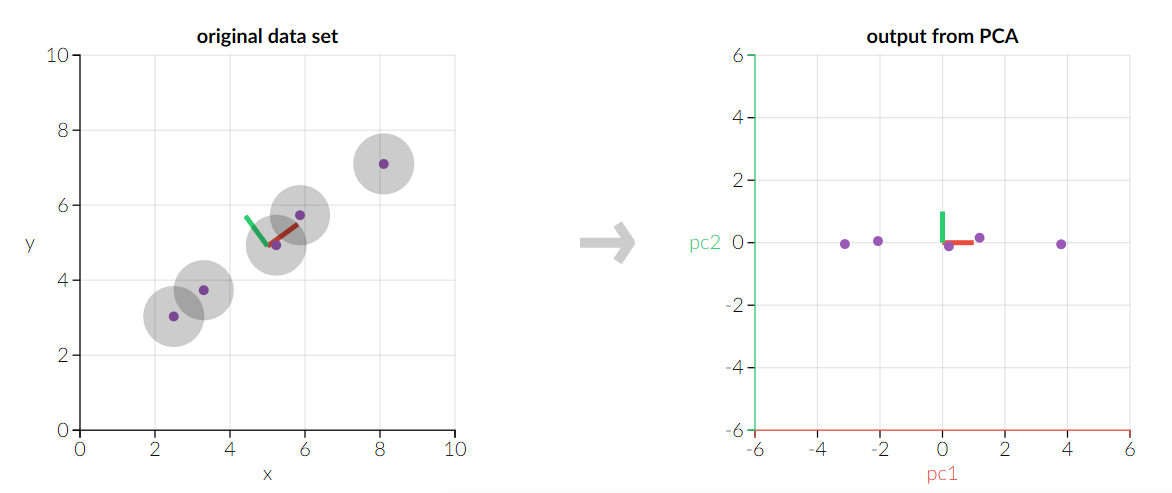
Method¶
Observation set $X$ contains $N$ samples and each sample $x_n \in R^p$. Transformation matrix $W$ contains $p$ column vectors, each vector $w_k \in R^p$. Principle component score $$s_{nk} = x_n w_k$$
In order to maximize variance, the first weight vector $w_1$ thus has to satisfy $$w_1 = \arg\max_{w_1} \sum_n s_{nk}^2=\arg\max_{w_1} W^T X^T X W,$$ $$s.t. ||W||=1$$
Since $w_1$ has been defined to be a unit vector, it equivalently also satisfies $$w_1 = \arg\max_{w_1} \frac{W^T X^T X W}{W^T W}$$
A standard result for a positive semidefinite matrix such as $X^T X$ is that the maximum possible value is the largest eigenvalue of the matrix, which occurs when $w_1$ is the corresponding eigenvector.
The full principal components decomposition of X can therefore be given as $$T = XW$$ where W is a p-by-p matrix of weights whose columns are the eigenvectors of $X^T X$.
Principal component analysis is also a technique for dimension reduction. It combines our input variables in a specific way, then we can drop the “least important” variables while still retaining the most valuable parts of all of the variables.
Algorithm¶
- Take the matrix of independent variables $X$ and, for each column, subtract the mean of that column from each entry and obtain $Z$. (This ensures that each column has a mean of zero.)
- Take the matrix $Z$, transpose it, and multiply the transposed matrix by $Z$. The resulting matrix is the covariance matrix $Z^T Z$.
- Calculate the eigenvectors and their corresponding eigenvalues of $Z^{T}Z$.
- Take the eigenvalues $λ_1, λ_2, …, λ_p$ and sort them from largest to smallest. In doing so, sort the eigenvectors in $W$ accordingly to obtain $W^*$.
- Calculate $Z^* = ZW^*$. This new matrix, $Z^*$, is a centered/standardized version of $X$ but now each observation is a combination of the original variables, where the weights are determined by the eigenvector.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
def pca_custom(X, k):
n, p = np.shape(X)
# make Z with mean zero
Z = X - np.mean(X, axis=0)
# calculate covariance maxtrix
covZ = np.cov(Z.T)
# calculate eigenvalues and eigenvectors
eigValue, eigVector = np.linalg.eig(covZ)
# sort eigenvalues in descending order
index = np.argsort(-eigValue)
# select k principle components
if k > p:
print ("k must lower than input data dimension!")
return 1
else:
# select k eigenvectors with largest eigenvalues
selectVector = eigVector[:, index[:k]]
T = np.matmul(Z, selectVector)
return T, selectVector
use_sklearn = True
# generate data
# x = np.random.randn(100, 20)
y = np.random.randn(20, 1)
x = np.matmul(y, [[1.3, -0.5]])
# set k
k = 2
# PCA
pcaX, selectVector = pca_custom(x, k)
print('PCA transformation matrix: ')
print(selectVector)
if use_sklearn:
z = x - np.mean(x, axis=0)
pcaResults = PCA(n_components=k).fit(z)
print ('PCA transformation matrix from sklearn:')
print(pcaResults.components_.T)
newX = np.matmul(z, pcaResults.components_.T)
print('original data')
plt.plot(x[:, 0], x[:, 1], 'ok')
plt.show()
print('After PCA')
plt.plot(pcaX[:, 0], pcaX[:, 1], 'or')
plt.show()
if use_sklearn:
print('After PCA from sklearn')
plt.plot(newX[:, 0], newX[:, 1], 'ob')
plt.show()